Grammar and FSA UAS

Grammar and FSA

GRAMMAR

Grammar adalah bentuk mesin abstrak yang dapat diterima (accept) untuk membangkitkan suatu kalimat otomata berdasarkan suatu kalimat berdasarkan suatu aturan tertentu.

Tata Bahasa (grammar) didefinisikan dengan empat (4) tupel

G = ({V, T, P, S}) dimana :
V = Himpunan simbol variabel / non terminal
T = Himpunan simbol terminal
P = Kumpulan aturan produksi
S = Simbol  awal

Mesin Abstrak Grammar

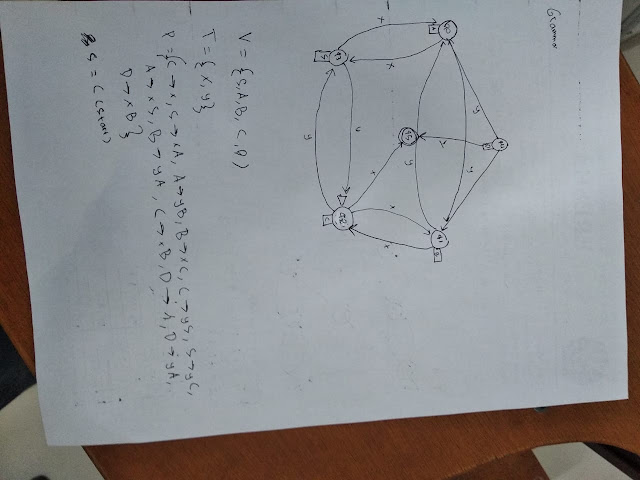
V = {S, A, B, C, D}

T = { x, y, λ }

P = { C→x, S→xA, A→yB, B→xC, C→yS, S→yC, A→xS, B→yA, C→xB, D→λ, D→yA, D→xB }

S = C (start)

Convert Right Linier Grammar to FA

FSA

Finite State Automata (FSA)

Finite State Automata (FSA) adalah mesin abstrak berupa sistem model matematika dengan masukan dan keluaran diskrit yang dapat mengenali bahasa paling sederhana (bahasa reguler) dan dapat diimplementasikan secara nyata.

Bahasa yang paling sederhana adalah bahasa reguler (tipe 3). Mesin yang bisa mengenalinya adalah Finite Automata. Finite Automata adalah mesin komputasi. Pada bahasan ini mesin komputasi yang dimaksud adalah mesin abstrak bukan mesin fisik, namun memadai untuk diimplementasikan secara nyata.

DEFINISI SECARA FORMAL

Secara formal FSA dinyatakan dengan 5-tuple atau M =(Q, Σ, δ, q₀, F):

1. Q = himpunan state/kedudukan

2. Σ = abjad, himpunan simbol input

3. δ = transition function

4. q₀ ∈ Q = start state

5. F ⊆

Q = set of accept (or final) states

v  Gambar di atas disebut diagram keadaan M1

v  Ia memiliki enam status, berlabel q0,q1, q2, q3, q4 dan q5

v  Status awal, q2, ditunjukkan oleh panah yang menunjuknya entah dari mana

v  Status terima, q5, adalah negara dengan lingkaran ganda

v  Panah yang berpindah dari satu kondisi ke kondisi lain disebut transisi

Kita dapat menggambarkan secara formal dengan menulis M1 = (Q, Σ, δ, q0, F)), di mana:

1. Q=  { q0, q1, q2, q3, q4, q5, q6 }
2. Σ = { 0, 1 }
3. δ digambarkan sebagai :

4. q0 adalah kondisi awal, dan
5. F = {q0}

Multiple Run

 Lembar Jawaban